The Scientific Prediction of Outcomes in Classical Roulette
Casino games always captured the interest of scientists and mathematicians, as they raised problems and questions regarding the possibility to predict the outcome of a game or to devise strategies by which a player would gain advantage over the house. Such questions can only be answered in a scientific framework. During the history of gambling there were several works in the academic community dedicated to such answers.
Roulette, as the oldest and most popular casino game, in its classical physical form has been subject to scientific investigation from the nineteenth century to present days. Since this game is entirely deterministic (that is, a particular outcome is caused by a multitude of physical factors and circumstances that we can or cannot account for) and is still a game of pure luck, where optimal strategies do not exist, the theoretical effort has been focused on predicting where the ball will land.
In this article we will see what this theoretical endeavor consisted of and what was the simplest and most effective approach to scientifically predict the outcome of a classical roulette game.
Landmarks in the history of the scientific investigation of roulette
We have to note from the beginning that there are two possible methods for predicting the outcome of a roulette on a scientific basis:
- One is by exploiting the information provided by an unbalanced, biased, or imperfect wheel – call it the statistical method.
- The other is by theoretically modeling the mechanical system where the spin of both the ball and wheel has a deterministic nature – call it the deterministic method.
Analyzing roulette data and exploiting them

In 1873, an English mechanic and amateur mathematician named Jagger found that slight imperfection in a roulette wheel could result in profitable play. The tale says that he went to the casino of Monte Carlo with six assistants, where they noted down the outcome of each spin at six tables over a period of five weeks. Analysis of the data revealed that for each wheel there was a unique bias that favored certain numbers as outcomes. Exploiting these weaknesses, he played profitably for a week before the casino management shuffled the wheels between tables. Even so, he soon observed various distinguishing features of the individual wheels and was able to follow them between tables, winning consistently.
Eventually, the casino managed to redistribute the individual partitions between pockets. It is the first documented evidence of someone skilled using the statistical method of predicting the outcome of an imperfect roulette wheel.
In 1947, two students from Chicago University, Albert Hibbs and Roy Walford, found irregularities in the roulette wheels of some local casinos and exploited them.
The work of these pioneers has been given a rigorous theoretical backup in 1982, when mathematician Stewart Ethier provided an applicative statistical framework by which one can test for irregularities in the observed outcomes of a roulette wheel and the equations providing the favored outcomes.
Struggling with the physics of roulette and measurements
In an academic paper published in 1969, mathematician Edward Thorpe (the father of the card-counting optimal strategy in blackjack) described two methods for deterministic prediction of the roulette outcome. He found that, if the wheel is not perfectly level, then there is a relatively large region of the frame which the ball will not fall onto the spinning wheel. By exploiting this information it is possible to raise the expected return to a positive +15% (+44% in the case of using a pocket-sized computer doing the measurements and computations), from the usual negative expectation of -2.70% (or -5.26%). Actually, a tilt of only 0.2º is more than sufficient for that to happen and, by studying Las Vegas roulette wheels, Thorpe and his collaborators observed this condition is met in about one third of wheels.
Another games mathematician, Richard Epstein, described his deterministic prediction experiments in his 1967 book. He claimed that by measuring the angular velocity of the ball relative to the wheel, he was able to correctly predict the half of the wheel into which the ball would fall. The principle grounding this prediction method is that the initial velocity (momentum) of the ball is not essential and the problem reverts to predicting when the ball will leave the outer (fixed) rim, as this will always occur at a fixed velocity.
Several scientific attempts to devise an accurate method of deterministic prediction followed the work of Thorpe and Epstein. While their principles are about the same and unquestionable, each theoretical account has its own degree of complexity and capacity to describe the real mechanical phenomenon. Such differences are reflected of course in the degree of accuracy of the prediction, but also in applicability. A first condition for such prediction systems to work is that the physical quantities representing the initial conditions are measurable and the measurements are accurate. This is the reason why the technology of measurement and computation used is essential. In addition, too many variables describing the phenomenon – while contributing to the adequacy of the model and accuracy of the results – pose practical problems to application.
Compromising between simplicity, applicability, and accuracy
Theoretical setup
The main principles and idealizations grounding Small and Kong Tse’s model are:
- The deflectors are evenly distributed around the stator at constant radius.
- The angular position of the ball spinning in the rim decreases only due to friction.
- Time is considered as the essential variable (and not position).
- Each spin of the ball determines only the time spent in the rim. The ball will leave the rim at the same velocity each time. The descent of the ball from this point to the deflectors will thus be identical.
- The exact position of the wheel when the ball reaches a deflector is considered random, but will depend only on the angular position of the wheel at the time of hitting the deflector.
The model for the level table describes the dynamical system as working in four stages:
- Ball rotates in the rim.
- Ball leaves the rim.
- Ball rotates freely on the stator.
- Ball reaches the deflectors.
Parameters and variables
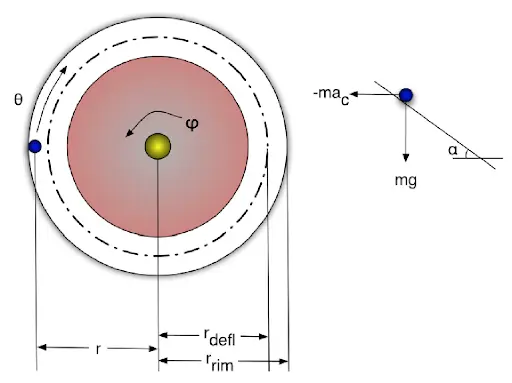
The roulette wheel is schematically depicted in the above figure, where its dimensions are expressed as the radiuses of the circles present in the construction of the wheel: marginal edge, rim, and deflector. The number of deflectors is also a parameter (N). Another parameter is the incline of the stator relative to the level plane (α) and the mass of the ball (m).
The main variables of the dynamical system are: the position of the ball in polar coordinates (θ), namely the angle that the ball makes with the center relative to a reference position – say, a particular pocket like 0), the angular position of the wheel relative to the same reference position (φ), and the radial acceleration (ac).
Derivation and inference
For a given initial motion of ball and wheel (described as a function of r, θ, φ, and the derivatives of the last two variables), the aim was to find the time tdefl at which r = rdefl . That time is assumed the time that the ball hits a deflector on the stator and drops onto the (still spinning) wheel. The exact position of the wheel when the ball reaches the deflectors is random but will depend only on φ(tdefl). Depending on where the actual deflectors are when the ball first comes within range, the radial distance until the ball actually deflects will be uniformly distributed on the interval (0, 2π/N).
By manipulating mathematically the equations of motion for the ball and wheel in the four mentioned stages of the dynamical system, the authors expressed the time when the ball reach a deflector. Then, they computed the instantaneous angular position of the ball and the wheel at the time it reaches a deflector, to obtain the angular location on the wheel directly below the point at which the ball strikes a deflector. The distribution of the resting place of the ball will depend only on this latter value.
For the case of a crooked table, the model is different, but relies on the same physical principles, and a new variable – the tilt angle – is employed in the equations.
For a tilted roulette wheel, one can expect that the ball will favor leaving the rim on one half of the wheel. To a good approximation, the point at which the ball will leave the rim follows a uniform distribution over less that half of the circumference. In that case, the problem of predicting the final resting place reverts to the problem of predicting the position of the wheel at the time the ball leaves the rim.
Manual measurement
Obviously the presented prediction model (as well as any other of this kind) can only be applied successfully if the user makes accurate measurements of the physical quantities reflecting the initial conditions. This requirement specifically refers to velocities and accelerations (as the wheel dimensions are supposed to be easily retrievable) and in present days these tasks of measuring and computing can be fulfilled by an application on a smartphone. However, this action renders the actual measurement very difficult, as the user must not raise any suspicion for the casino’s staff.
The authors proposed a manual measurement supposed to replace the electronic measurement. The idea was to record the time (in seconds) at which ball and wheel pass a fixed point. In their experiment they recorded from two spins of the wheel and 20 successive spins of the ball the timings T(i) and T(i + 1) of two successive revolutions, which actually are indirect measurements for the angular velocity observed over one complete rotation. From the relationship between the two Ts, one can determine the angular acceleration and deceleration.
The accuracy of such manual measurement is dependent on the hand-eye coordination of the observer. The manual measurement can replace only the measuring function of the alleged prediction device, which still remains necessary for computation.
Final thoughts
Small and Kong Tse’s prediction model is very simple compared to other more sophisticated models and simplicity is a crucial criterion when it comes to the effectiveness of concrete applications. At the time the paper of Small and Kong Tse was published, most of the land-based casinos had already implemented the new shuffling technology based on RNG. As always, the casino industry responded with countermeasures anytime a brilliant mind managed to exploit detected breaches in randomness and functionality of the games.
Once players came to use electronic devices for measurements on physical roulette, the casinos moved to incorporate random rotor speed wheels, making any deterministic prediction impossible. Electronic roulette based on RNG then spread across casinos, including land-based. Many casinos today offer classical croupier-spun roulette as there is still demand for them. This is actually the very narrow domain of application for theoretical models of prediction like the one presented. The effectiveness of such applications still depends on factors beyond the theory, including skills and local circumstances, like the level of security of each casino.
References:
- Epstein, R. A. (1967). The Theory of Gambling and Statistical Logic. New York: Academic Press. {Link}
- Ethier, S. N. (1982). Testing for favorable numbers on a roulette wheel. Journal of American Statistical Association, Vol. 77, 660–665. {Link}
- Small, M., & Tse, C. K. (2012). Predicting the outcome of roulette. Chaos: an interdisciplinary journal of nonlinear science, 22(3), 033150. {Link}
- Thorp, E. O. (1969). Optimal gambling systems for favorable games. Review of the International Statistical Institute, Vol. 37, 273–293. {Link}

